Diện tích hình thang cân
Hình thang cân là một loại hình thang đặc biệt, trong đó hai cạnh bên bằng nhau và hai góc kề mỗi đáy bằng nhau. Hình thang cân có trục đối xứng đi qua trung điểm hai đáy, giúp dễ tính toán và áp dụng công thức.
Đặc điểm chính của hình thang cân
Hai cạnh bên bằng nhau
AD=BC
Hai đáy song song
AB // CD
Góc kề đáy bằng nhau
∠ A=∠ B, ∠ C=∠ D
Đối xứng qua trục trung trực
Hình thang cân có trục đối xứng đi qua trung điểm hai đáy, chia hình thang thành hai tam giác cân bằng nhau.
Các tam giác bên là tam giác cân
Khi kẻ đường cao từ đỉnh xuống đáy, ta có hai tam giác cân, thuận tiện để tính diện tích và các yếu tố hình học khác.

Công thức tính diện tích của hình thang cân?Công thức cơ bản
Nếu hình thang cân có:
Đáy lớn=AB=a
Đáy nhỏ=CD=b
Chiều cao=h (khoảng cách giữa hai đáy)
Diện tích S được tính bằng công thức:
S=½ × (a + b) × h
S: diện tích của hình thang cân
a, b: độ dài hai đáy
h: chiều cao (vuông góc giữa hai đáy)
Công thức khi biết cạnh bên và đáy
Nếu hình thang cân có:
Cạnh bên=c
Đáy lớn=a, đáy nhỏ=b
Chiều cao h có thể tính bằng công thức theo định lý Pythagore:
h=√ [c² - ((a - b)/2)² ]
Sau đó thay vào công thức diện tích:
S=½ × (a + b) × h
Bài tập 1: Tính diện tích khi biết hai đáy và chiều cao
Đề bài: Một hình thang cân có đáy lớn a=12 cm, đáy nhỏ b=8 cm, và chiều cao h=5 cm. Tính diện tích của hình thang cân.
Lời giải:
Bước 1: Nhận xét
Hình thang cân có hai đáy song song và chiều cao vuông góc giữa hai đáy là h=5 cm.
Công thức diện tích của hình thang cân:
S=½ × (a + b) × h
Bước 2: Thay số vào công thức
S=½ × (12 + 8) × 5
S=½ × 20 × 5
S=10 × 5=50 cm²
Đáp án:
S=50 cm²
Ví dụ bài tập tính diện tích của hình thang cân kèm lời giải.Bài tập 2: Tính diện tích khi biết đáy và cạnh bên
Đề bài: Một hình thang cân có đáy lớn a=14 cm, đáy nhỏ b=10 cm, và cạnh bên c=5 cm. Tính diện tích hình thang.
Lời giải:
Bước 1: Tính chiều cao
Chiều cao h được tính từ định lý Pythagore:
h=√ [c² - ((a - b)/2)² ]
Thay số:
h=√ [5² - ((14 - 10)/2)² ]=√ [25 - 4]=√ 21 ≈ 4, 58 cm
Bước 2: Áp dụng công thức diện tích
S=½ × (a + b) × h
S=½ × (14 + 10) × 4, 58
S=½ × 24 × 4, 58 ≈ 12 × 4, 58 ≈ 54, 96 cm²
Đáp án:
S ≈ 54, 96 cm²
Bài tập 3: Bài toán thực tế
Đề bài: Một mảnh đất hình thang cân có đáy lớn a=20 m, đáy nhỏ b=12 m, và cạnh bên c=7 m. Tính diện tích mảnh đất.
Lời giải:
Bước 1: Tính chiều cao
h=√ [c² - ((a - b)/2)² ]=√ [7² - ((20 - 12)/2)² ]=√ [49 - 16]=√ 33 ≈ 5, 74 m
Bước 2: Tính diện tích
S=½ × (a + b) × h=½ × (20 + 12) × 5, 74=½ × 32 × 5, 74 ≈ 16 × 5, 74 ≈ 91, 84 m²
Đáp án:
Diện tích mảnh đất ≈ 91, 84 m²
Bước 3: Nhận xét
Việc kẻ đường cao từ đỉnh xuống đáy tạo ra hai tam giác vuông cân giúp tính nhanh chiều cao.
Hình thang cân giúp tính diện tích dễ dàng nhờ tính chất đối xứng.
Mẹo giúp ghi nhớ công thức diện tích của hình thang cân nhanhDưới đây là một số mẹo giúp ghi nhớ công thức diện tích của hình thang cân nhanh và hiệu quả, đặc biệt hữu ích cho học sinh, sinh viên:
Hiểu bản chất trước khi học thuộc
Hình thang cân có hai đáy song song và chiều cao h vuông góc giữa hai đáy.
Diện tích hình thang=½ × (tổng hai đáy) × chiều cao, tức là:
S=½ × (a + b) × h
Khi hiểu tại sao lại nhân nửa với tổng đáy và chiều cao, bạn sẽ dễ nhớ lâu hơn.
Liên tưởng trực quan
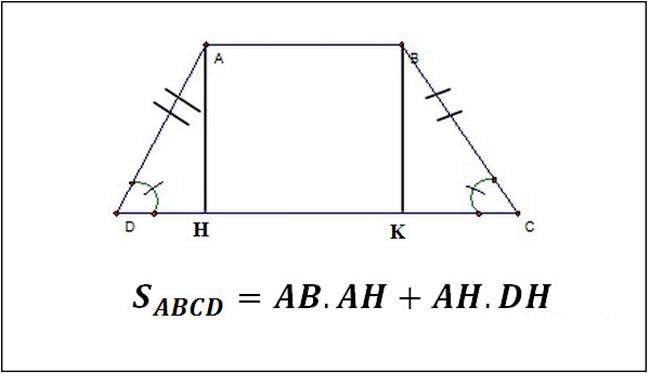
Tưởng tượng chia hình thang thành hình chữ nhật và hai tam giác vuông cân:
Hình chữ nhật=chiều cao × đáy nhỏ
Hai tam giác vuông cân=½ × chiều cao × (đáy lớn – đáy nhỏ)
Cộng lại ra S=½ × (a + b) × h
Hình ảnh trực quan này giúp não tự nhớ công thức.
Dùng câu nói ngắn gọn dễ thuộc
Tạo câu nhớ:
“ Diện tích của hình thang cân=nửa tổng đáy nhân chiều cao”
Khi cần tính, chỉ cần nhớ câu này là áp dụng công thức ngay.
Ghi nhớ khi biết cạnh bên
Khi biết cạnh bên c và hai đáy, cần tính chiều cao h bằng Pythagore:
h=√ [c² - ((a - b)/2)² ]
Sau đó thay vào công thức:
S=½ × (a + b) × h
Câu nhớ: “ Chiều cao từ cạnh bên, diện tích=nửa tổng đáy × h”
Thực hành nhiều ví dụ
Tính diện tích với nhiều bộ số liệu khác nhau: đáy lớn, đáy nhỏ, chiều cao, cạnh bên.
Khi làm nhiều bài, công thức sẽ tự in sâu vào trí nhớ, không cần học thuộc lòng.
Liên kết với kiến thức hình học khác
Từ tam giác vuông cân trong hình thang cân, bạn dễ nhớ cách tính chiều cao bằng Pythagore.
Việc liên kết với tam giác, định lý Pythagore giúp ghi nhớ công thức nhanh và chính xác hơn.
Kết hợp các mẹo: hiểu bản chất, liên tưởng trực quan, câu nói ngắn gọn, thực hành nhiều, liên kết kiến thức, bạn sẽ nhớ công thức diện tích của hình thang cân nhanh và áp dụng dễ dàng trong mọi bài toán.
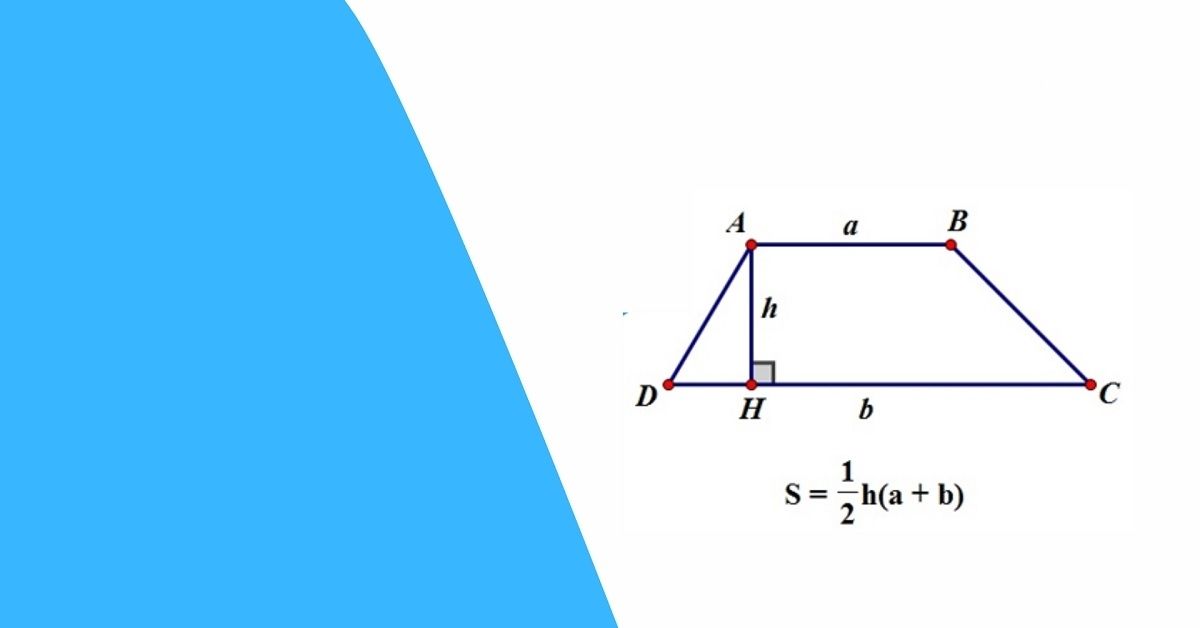
Diện tích hình thang cân áp dụng trong thực tếDiện tích của hình thang cân không chỉ là kiến thức lý thuyết mà còn được áp dụng rộng rãi trong xây dựng, kỹ thuật, thiết kế và đời sống hàng ngày. Dưới đây là một số ứng dụng thực tế:
Xây dựng và kiến trúc
Tính diện tích mái nhà tam giác hoặc mái chéo hình thang:
Nhiều mái nhà thiết kế dạng hình thang cân (đáy lớn nhỏ khác nhau), diện tích cần lợp được tính nhanh bằng công thức:
S=½ × (a + b) × h
Tính diện tích sân vườn hoặc lối đi:
Khi mảnh đất được chia thành các mảnh hình thang cân, diện tích từng mảnh được tính nhanh chóng để dự trù vật liệu và chi phí.
Kỹ thuật và cơ khí
Gia công kim loại, gỗ hoặc vật liệu xây dựng:
Cắt các chi tiết hình thang cân, diện tích giúp tính lượng vật liệu cần dùng.
Thiết kế khung, giá đỡ hoặc bộ phận máy móc:
Hình thang cân thường được dùng vì tính đối xứng và ổn định, thuận tiện cho kỹ thuật và cơ học.
Thiết kế đồ họa và nghệ thuật
Trang trí và thiết kế mô hình:
Các hình thang cân xuất hiện trong logo, họa tiết, mô hình 2D hoặc 3D.
Tính lượng vật liệu:
Diện tích giúp ước lượng giấy, decal, sơn cần dùng cho các mô hình.
Trường hợp thực tế khác
Đo diện tích đất hoặc hồ bơi:
Khi đất hoặc khu vực hình thang cân, diện tích giúp dự trù chi phí và vật liệu.
Tính tải trọng hoặc trọng lượng vật liệu:
Trong cơ học, biết diện tích mặt cắt hình thang cân giúp tính lực hoặc áp lực tác động lên vật liệu.
Trên đây, chúng tôi đã giới thiệu chi tiết về diện tích của hình thang cân, bao gồm định nghĩa, đặc điểm, công thức tính diện tích khi biết đáy và chiều cao hoặc cạnh bên, cùng các ví dụ minh họa kèm lời giải chi tiết. Bên cạnh đó, các mẹo ghi nhớ công thức và ứng dụng thực tế cũng giúp học sinh, sinh viên nắm chắc kiến thức và áp dụng linh hoạt trong bài tập cũng như đời sống hàng ngày. Hy vọng bài viết sẽ là tài liệu tham khảo hữu ích, giúp các bạn học tập hiệu quả, ghi nhớ công thức lâu dài và tự tin giải quyết mọi bài toán liên quan đến hình thang cân một cách nhanh chóng và chính xác.