Diện tích hình thang cân
Hình thang cân là gì và đặc điểm nhận biết
Hình thang cânlà một hình tứ giác đặc biệt, trong đó hai cạnh bên có độ dài bằng nhau. Nhờ tính chất này, hình thang cân tạo nên sự đối xứng qua đường thẳng đi qua trung điểm của hai đáy. Khi vẽ hình, bạn sẽ dễ dàng nhận ra rằng nếu gập hình theo đường đối xứng đó, hai nửa sẽ khớp với nhau hoàn toàn. Đây chính là sự cân đối đặc trưng mà các loại hình thang khác không có.
Đặc điểm này khiến hình thang cân vừa quen thuộc vừa dễ học, bởi học sinh chỉ cần nhớ một số tính chất cơ bản là có thể áp dụng ngay vào việc giải toán. Ngoài ra, trong nhiều bài toán hình học, hình thang cân thường được lựa chọn làm ví dụ vì nó đơn giản nhưng lại chứa đựng nhiều ứng dụng.
Ý nghĩa của diện tích của hình thang cân
Diện tích của hình thang cânchính là phần mặt phẳng được giới hạn bởi bốn cạnh của hình. Việc tính diện tích không chỉ mang giá trị học thuật mà còn là một kỹ năng thực tế. Chẳng hạn, khi đo một mảnh đất có hình thang cân, việc biết diện tích giúp bạn tính toán chi phí xây dựng. Khi thiết kế một chiếc bàn hay cánh cửa có hình dáng này, diện tích giúp xác định vật liệu cần thiết. Vì thế, công thức diện tích của hình thang cân là một trong những công thức cơ bản nhưng rất hữu dụng trong cuộc sống.

Diện tích hình thangCông thức tính toán chuẩn xác
Công thức diện tích của hình thang cân được viết như sau: S=((a + b) × h) / 2 Trong đó, alà cạnh đáy lớn, blà cạnh đáy nhỏ, và hlà chiều cao. Điểm quan trọng là phải xác định chính xác đâu là đáy lớn, đâu là đáy nhỏ. Chiều cao h là đoạn vuông góc kẻ từ một đỉnh nằm trên đáy lớn xuống đáy nhỏ.
Công thức trên không chỉ áp dụng cho hình thang cân mà còn đúng cho mọi loại hình thang. Tuy nhiên, trong trường hợp hình thang cân, việc dựng đường cao đơn giản hơn nhờ sự đối xứng, giúp cho quá trình tính toán trở nên nhanh chóng.
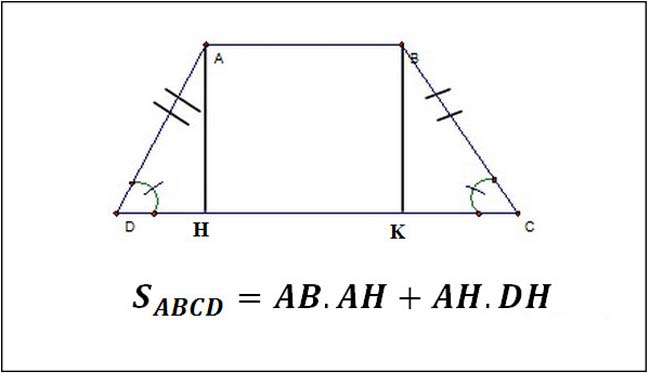
Diện tích hình thang cânKhi đề bài không cho sẵn chiều cao
Trong nhiều trường hợp, đề toán sẽ không cung cấp trực tiếp chiều cao. Lúc này, bạn phải sử dụng mối liên hệ giữa cạnh bên và hiệu số của hai đáy để tìm h.
Giả sử hình thang cân có đáy lớn bằng 18 cm, đáy nhỏ bằng 10 cm, cạnh bên bằng 13 cm. Hiệu số giữa hai đáy là 8, chia đôi ta được 4. Từ đó, chiều cao h sẽ được tính bằng công thức h=√ (c² - d² ), trong đó c là cạnh bên và d là nửa hiệu hai đáy. Thay số ta có h=√ (13² - 4² )=√ (169 - 16)=√ 153 ≈ 12, 37 cm. Sau khi có chiều cao, ta tính diện tích S=((18 + 10) × 12, 37) / 2 ≈ 173, 18 cm² .
Bài toán gắn với thực tế
Hãy tưởng tượng bạn muốn thiết kế một tấm biển quảng cáo có hình dạng hình thang cân. Đáy lớn của biển dài 3 mét, đáy nhỏ dài 2 mét, cạnh bên dài 1, 5 mét. Để biết diện tích bề mặt cần in, bạn trước tiên phải tìm chiều cao. Hiệu số giữa hai đáy là 1 mét, chia đôi được 0, 5 mét. Khi đó h=√ (1, 5² - 0, 5² )=√ (2, 25 - 0, 25)=√ 2 ≈ 1, 41 mét. Áp dụng công thức diện tích, ta có S=((3 + 2) × 1, 41) / 2=3, 53 mét vuông. Nhờ vậy, bạn biết được lượng vật liệu in cần dùng cho tấm biển quảng cáo.
:quality(75)/small/cong_thuc_tinh_dien_tich_hinh_thang_thum_930df4fc68.jpg)
Hình thangTrong giáo dục và thi cử
Diện tích hình thang cân là kiến thức thường xuyên xuất hiện trong các bài tập toán từ bậc tiểu học cho đến trung học. Các đề thi không chỉ yêu cầu áp dụng trực tiếp công thức mà còn kết hợp với các yếu tố khác như tìm chiều cao, sử dụng tính chất tam giác vuông, hoặc so sánh với diện tích các hình khác. Điều này giúp học sinh rèn luyện khả năng tư duy logic và áp dụng linh hoạt công thức vào nhiều tình huống khác nhau.
Trong xây dựng và kiến trúc
Trong lĩnh vực xây dựng, hình thang cân có mặt ở nhiều hạng mục. Một ô cửa sổ mái, một phần mái nhà hoặc mảnh đất có hình dạng đặc thù đều có thể được mô tả bằng hình thang cân. Khi cần ước tính diện tích để mua vật liệu như kính, ngói, gạch lát, công thức tính diện tích hình thang cân sẽ được áp dụng. Ví dụ, một ô cửa sổ có đáy lớn 2 mét, đáy nhỏ 1, 2 mét, chiều cao 1, 5 mét. Áp dụng công thức, diện tích bằng ((2 + 1, 2) × 1, 5) / 2=2, 4 mét vuông. Kết quả này cho phép người thợ tính toán lượng kính cần mua mà không bị thừa hoặc thiếu.
Trong đời sống hằng ngày
Ngay cả trong các hoạt động thường ngày, công thức diện tích của hình thang cân vẫn hữu ích. Khi bạn muốn cắt một tấm vải để may áo, trải bàn hay làm rèm cửa có hình dáng hình thang cân, việc tính toán chính xác diện tích giúp tiết kiệm nguyên liệu. Khi đo một mảnh đất vườn có hình dạng bất đối xứng nhưng gần giống hình thang cân, việc quy đổi về công thức diện tích giúp bạn dễ dàng ước lượng diện tích thực tế. Nhờ vậy, toán học không còn xa rời cuộc sống mà trở thành công cụ thực tế và cần thiết.
Diện tích hình thang cân là một trong những công thức cơ bản và cần thiết của hình học. Nhờ sự đơn giản và tính ứng dụng cao, công thức này xuất hiện cả trong sách giáo khoa lẫn trong đời sống thực tế. Việc nắm vững cách tính diện tích của hình thang cân không chỉ giúp bạn học tốt môn toán mà còn hỗ trợ nhiều trong xây dựng, thiết kế và các hoạt động hằng ngày. Hãy luyện tập thường xuyên qua nhiều ví dụ khác nhau để biến công thức này thành kỹ năng quen thuộc.>> Xem thêm: Dấu hiệu chia hết cho 7