Diện tích tứ giác
Định nghĩa tứ giác
Tứ giác là một hình phẳng được giới hạn bởi bốn đoạn thẳng, trong đó mỗi đoạn thẳng được gọi là một cạnh và bốn điểm nối lại với nhau được gọi là bốn đỉnh. Tứ giác là một trong những hình học phẳng cơ bản nhất, được giới thiệu sớm trong chương trình toán học phổ thông.
Một tứ giác luôn có tổng bốn góc trong bằng 360 độ. Từ đặc điểm này, nhiều công thức tính diện tích hình tứ giác đã được xây dựng và phát triển để giải các bài toán khác nhau.
Các loại tứ giác thường gặp
Trong hình học, có nhiều loại tứ giác đặc biệt như hình vuông, hình chữ nhật, hình thoi, hình thang hay hình bình hành. Mỗi loại tứ giác đều có công thức tính diện tích riêng, giúp quá trình giải toán trở nên nhanh chóng và chính xác. Việc nắm rõ từng loại tứ giác sẽ là nền tảng quan trọng khi học sinh tìm hiểu cách tính diện tích hình tứ giác trong từng trường hợp cụ thể.
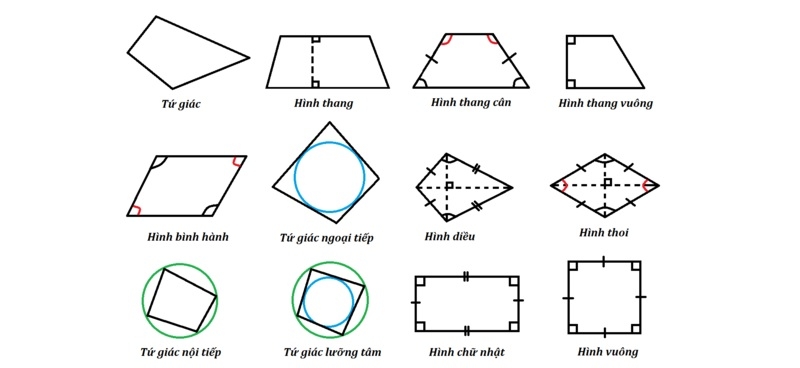
Các loại tứ giác phổ biến trong toán họcTrường hợp tứ giác đơn giản
Đối với các tứ giác đặc biệt như hình vuông, hình chữ nhật hay hình thoi, công thức tính diện tích khá đơn giản. Với hình vuông, diện tích được tính bằng cạnh nhân với cạnh. Với hình chữ nhật, diện tích bằng chiều dài nhân với chiều rộng. Hình thoi có diện tích bằng tích hai đường chéo chia cho hai.
Những công thức này đều dễ nhớ và áp dụng trực tiếp khi bạn biết các kích thước cơ bản của hình. Đây cũng chính là những trường hợp thường xuyên xuất hiện trong sách giáo khoa.
Trường hợp tứ giác bất kỳ
Đối với tứ giác không có dạng đặc biệt, việc tính diện tích trở nên phức tạp hơn. Một trong những công thức phổ biến nhất là công thức Bretschneider, được áp dụng khi biết độ dài bốn cạnh và hai đường chéo hoặc hai góc đối diện. Công thức này xuất phát từ việc mở rộng công thức Heron của tam giác sang tứ giác.
Ví dụ minh họa
Giả sử có tứ giác được chia thành hai tam giác bởi đường chéo AC. Nếu tam giác ABC có diện tích 20 cm² và tam giác ACD có diện tích 15 cm² , thì diện tích hình tứ giác ABCD bằng 35 cm² . Cách tính này giúp bạn dễ dàng xử lý những tứ giác không đều hoặc khó đo trực tiếp.
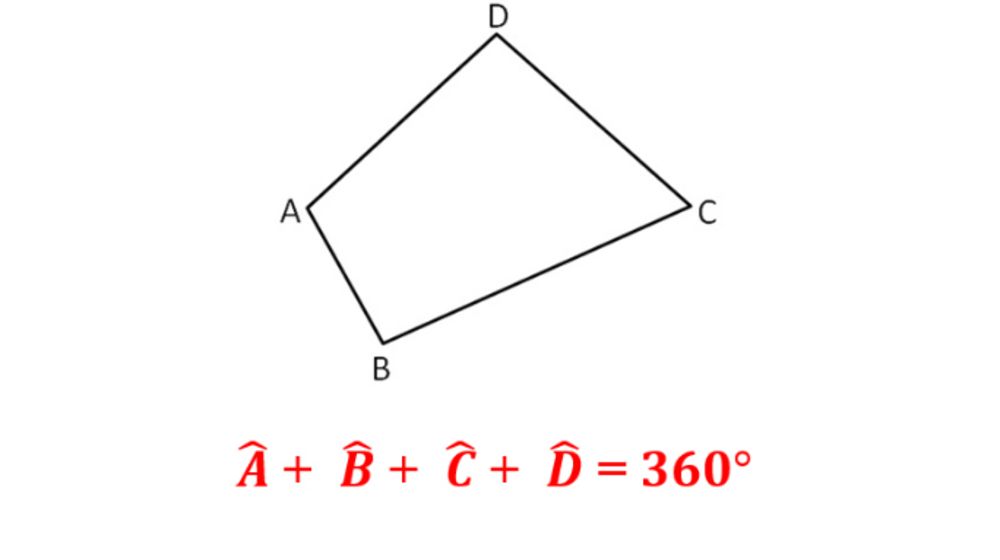
Tứ giácDiện tích hình thang
Hình thang là tứ giác có hai cạnh đối song song. Diện tích hình thang được tính theo công thức: S=(a + b) × h / 2, trong đó a và b là hai đáy song song, h là chiều cao.
Diện tích hình bình hành
Hình bình hành có hai cạnh đối song song và bằng nhau. Công thức tính diện tích hình bình hành là S=a × h, trong đó a là cạnh đáy và h là chiều cao kẻ từ đỉnh đối diện.
Diện tích hình vuông và hình chữ nhật
Hình vuông là trường hợp đặc biệt của hình chữ nhật. Diện tích hình chữ nhật bằng chiều dài nhân chiều rộng. Khi hai cạnh bằng nhau, công thức trở thành S=a × a, chính là công thức tính diện tích hình vuông.
Diện tích hình thoi
Hình thoi có bốn cạnh bằng nhau. Công thức tính diện tích hình thoi là S=d1 × d2 / 2, trong đó d1 và d2 là hai đường chéo.
Ý nghĩa của việc nắm rõ công thức
Khi biết được công thức tính diện tích từng loại tứ giác, bạn có thể giải quyết hầu hết các bài toán hình học phẳng. Việc phân loại và áp dụng đúng công thức là chìa khóa để tiết kiệm thời gian và tránh sai sót.
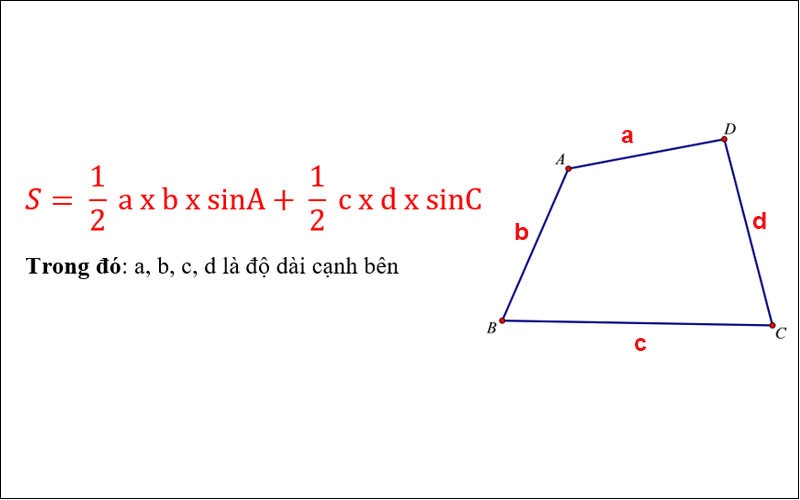
Các công thức diện tích hình tứ giác quen thuộcỨng dụng trong học tập
Trong các kỳ thi toán, bài tập về diện tích hình tứ giác thường xuyên xuất hiện để kiểm tra khả năng vận dụng công thức của học sinh. Việc nắm chắc công thức giúp bạn dễ dàng giải các bài toán từ đơn giản đến nâng cao.
Ứng dụng trong kiến trúc và xây dựng
Trong thực tế, diện tích tứ giác được dùng để tính toán diện tích bề mặt khi thiết kế nhà cửa, cầu đường, sân chơi hay công viên. Chẳng hạn, khi bạn cần lát gạch một khuôn viên hình thang, việc tính đúng diện tích giúp bạn mua đủ số lượng gạch mà không bị thừa hoặc thiếu.
Ứng dụng trong nông nghiệp và quy hoạch
Khi đo đạc diện tích đất đai, rất nhiều thửa đất có hình dạng giống tứ giác. Áp dụng công thức diện tích hình tứ giác giúp người nông dân và kỹ sư quy hoạch tính toán chính xác diện tích canh tác hoặc diện tích xây dựng.
Ý nghĩa thực tiễn
Việc nắm vững cách tính diện tích hình tứ giác cho thấy toán học không chỉ là kiến thức sách vở mà còn có giá trị ứng dụng thực tế rất cao. Từ lớp học đến công trường, từ bản vẽ đến đời sống thường ngày, diện tích hình tứ giác luôn là một trong những công cụ toán học hữu ích nhất.
Bài tập minh họa
Một tứ giác ABCD có đường chéo AC chia tứ giác thành hai tam giác. Nếu diện tích tam giác ABC bằng 24 cm² và diện tích tam giác ACD bằng 30 cm² , hãy tính diện tích tứ giác ABCD.
Lời giải: Diện tích tứ giác ABCD bằng diện tích tam giác ABC cộng diện tích tam giác ACD, kết quả là 24+30=54 cm² .
Bài tập thực tế
Một mảnh đất hình thang có đáy lớn dài 20 m, đáy nhỏ dài 10 m và chiều cao 8 m. Tính diện tích mảnh đất.
Lời giải: Áp dụng công thức hình thang, ta có S=(20 + 10) × 8 / 2=120 m² .
Diện tích tứ giác là một khái niệm quan trọng trong hình học, có thể tính toán bằng nhiều công thức khác nhau tùy vào loại tứ giác. Với tứ giác đặc biệt như hình vuông, hình chữ nhật, hình thoi hay hình thang, công thức đơn giản và dễ áp dụng. Với tứ giác bất kỳ, bạn có thể chia nhỏ thành tam giác hoặc áp dụng công thức tổng quát. Việc hiểu rõ và vận dụng chính xác cách tính diện tích hình tứ giác không chỉ giúp học tập hiệu quả mà còn mang lại nhiều giá trị trong thực tế, từ kiến trúc, quy hoạch đến nông nghiệp và đời sống thường ngày.>> Xem thêm: Diện tích hình thang cân