Số hạng là gì?
Trong toán học, số hạng là một thành phần trong một biểu thức hoặc một dãy số, được ngăn cách nhau bởi dấu cộng (+) hoặc dấu trừ (− ). Mỗi số hạng có thể là một số, một biến, hoặc tích của số và biến. Ví dụ, trong biểu thức 5x+3y − 7, các số hạng lần lượt là 5x, 3y và − 7.
Đặc điểm của số hạng
Trong toán học, số hạng có một số đặc điểm quan trọng giúp phân biệt và nhận diện trong biểu thức hoặc dãy số.
Số hạng trong biểu thức
Mỗi số hạng được tách biệt bởi dấu cộng (+) hoặc trừ (− ). Ví dụ trong biểu thức 7x² − 5x+3, ta có ba số hạng là 7x² , − 5x và 3.
Số hạng có thể là hằng số (chỉ chứa số), biến số, hoặc tích giữa số và biến.
Hệ số là phần số đứng trước biến, cũng được coi là một thành phần của số hạng, chẳng hạn trong 4y, hệ số là 4.
Số hạng trong đa thức và dãy số
Trong đa thức, các số hạng tạo thành toàn bộ cấu trúc của biểu thức.
Trong dãy số, số hạng chỉ ra vị trí cụ thể. Ví dụ, số hạng thứ 5 trong dãy số tự nhiên là 5.
Số hạng là gì có thể thay đổi theo quy luật, như trong cấp số cộng hoặc cấp số nhân.
Tính chất quan trọng
Số hạng có thể được cộng, trừ hoặc nhân theo các quy tắc đại số.
Chỉ những số hạng “ cùng loại” (chứa cùng biến và cùng số mũ) mới có thể cộng hoặc trừ trực tiếp với nhau.
Như vậy, số hạng vừa mang tính độc lập trong từng biểu thức, vừa đóng vai trò kết nối để tạo nên các dạng toán học lớn hơn như đa thức hay dãy số.
Số hạng trong dãy số
Trong toán học, số hạng là gì trong dãy số là mỗi phần tử xuất hiện trong một dãy đã được sắp xếp theo một quy luật nhất định. Mỗi số hạng thường được ký hiệu bằng một chữ cái kèm chỉ số, chẳng hạn như:
u1, u2, u3, … , un trong dãy số u.
a1, a2, a3, … , an trong dãy số a.
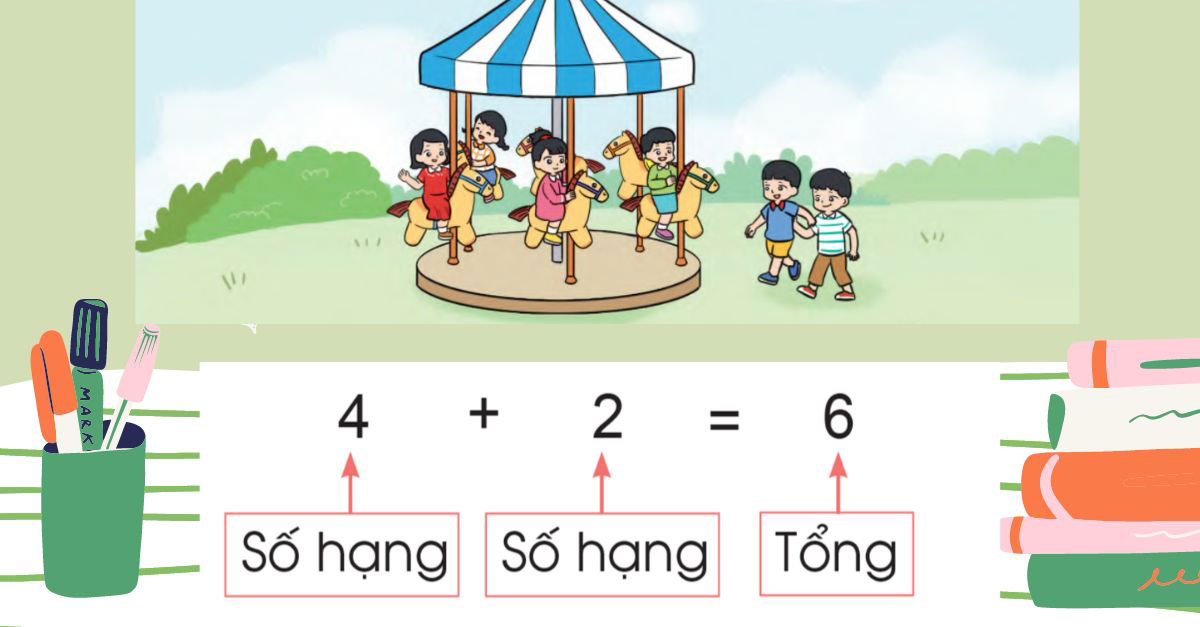 Số hạng trong toán học
Số hạng trong toán họcCác số hạng được sắp xếp theo một trật tự rõ ràng: từ số hạng đầu tiên đến số hạng thứ n.
Mỗi số hạng có thể được xác định thông qua công thức tổng quát hoặc bằng cách dựa vào số hạng trước đó.
Dãy số có thể là dãy số cộng, dãy số nhân hoặc dãy số bất kỳ khác.
Ví dụ minh họa
Dãy số tự nhiên: 1, 2, 3, 4, … → các số 1, 2, 3, 4 chính là các số hạng.
Dãy số cộng với số đầu là 3 và công sai bằng 2: 3, 5, 7, 9, … → số hạng tổng quát là:
u(n)=3+(n - 1) * 2
Dãy số nhân bắt đầu từ 2, công bội bằng 3: 2, 6, 18, 54, … → số hạng tổng quát là:
u(n)=2 * 3^(n - 1)
Số hạng trong dãy số giúp ta dễ dàng xác định vị trí, giá trị cụ thể của từng phần tử. Việc nắm rõ số hạng là gì còn quan trọng khi giải các bài toán về cấp số cộng, cấp số nhân, hoặc ứng dụng trong các bài toán thực tế như tính lãi suất, dự đoán sự tăng trưởng hay mô tả quy luật tự nhiên.
 Giờ học Toán
Giờ học ToánKhái niệm số hạng không chỉ xuất hiện trong các bài toán lý thuyết mà còn có nhiều ứng dụng thực tế trong đời sống và nghiên cứu khoa học. Việc hiểu và vận dụng số hạng là gì giúp giải quyết nhiều dạng bài toán, từ đơn giản đến phức tạp.
Trong toán học
Số hạng được dùng để xây dựng các dãy số như cấp số cộng, cấp số nhân. Từ đó, ta có thể tính toán nhanh giá trị của số hạng thứ n mà không cần viết hết toàn bộ dãy.
Hỗ trợ trong việc giải phương trình, chứng minh công thức và phân tích biểu thức toán học.
Là nền tảng để phát triển các khái niệm nâng cao hơn như giới hạn dãy số, chuỗi số và giải tích.
Trong thực tiễn
Tài chính – ngân hàng: số hạng giúp mô tả quy luật tăng trưởng của vốn đầu tư, tiền gửi tiết kiệm hay khoản vay theo từng kỳ hạn. Ví dụ, công thức số hạng trong cấp số nhân thường được dùng để tính lãi kép.
Khoa học và kỹ thuật: dãy số và số hạng được sử dụng để mô phỏng quá trình lặp đi lặp lại, chẳng hạn như dao động, tốc độ tăng trưởng dân số hoặc phân rã hạt nhân.
Thống kê và dự đoán: số hạng cho phép ước tính giá trị tương lai dựa trên quy luật của dãy số đã có, từ đó hỗ trợ phân tích xu hướng trong kinh tế hay dữ liệu xã hội.
Ví dụ minh họa
Trong cấp số cộng 2, 5, 8, 11, … , nếu muốn biết số hạng thứ 20, ta có công thức tổng quát:
u(n)=2+(n - 1) * 3
Khi n=20, ta tính được số hạng thứ 20 là 59, không cần viết cả dãy dài dòng.
 Số học trong toán
Số học trong toánĐể hiểu rõ hơn về khái niệm số hạng, bạn có thể tham khảo một số bài tập sau:
Bài 1
Cho dãy số: 4, 7, 10, 13, …
a) Xác định công sai của dãy.
b) Viết công thức số hạng tổng quát.
c) Tìm số hạng thứ 15 của dãy.
Bài 2
Một cấp số cộng có số hạng đầu là 5, công sai là 6.
a) Viết công thức số hạng tổng quát.
b) Tìm số hạng thứ 20.
Bài 3
Cho dãy số: 3, 6, 12, 24, …
a) Đây là dãy số gì?
b) Viết công thức số hạng tổng quát.
c) Tìm số hạng thứ 8.
Bài 4
Số hạng thứ n của một dãy số được cho bởi công thức:
u(n)=2n+1
a) Viết 5 số hạng đầu tiên của dãy.
b) Tính số hạng thứ 50.
Bài 5
Trong một cấp số cộng có số hạng đầu là -2, số hạng thứ 6 bằng 18.
a) Xác định công sai của dãy.
b) Tìm công thức số hạng tổng quát.
c) Tính số hạng thứ 12.