Diện tích tứ giác
Tứ giác là một hình phẳng trong hình học được tạo thành bởi bốn đoạn thẳng khi nối liền bốn điểm phân biệt. Các điểm này được gọi là bốn đỉnh, bốn đoạn thẳng nối liền các đỉnh gọi là bốn cạnh, và phần không gian giới hạn bởi bốn cạnh gọi là tứ giác. Điều kiện để tạo thành tứ giác là không có ba điểm nào trong bốn đỉnh thẳng hàng với nhau.

Học sinh trong giờ toán
Đặc điểm cơ bản của tứ giác
Tứ giác có bốn đỉnh và bốn cạnh, tạo thành bốn góc trong.
Tổng số đo bốn góc trong của tứ giác luôn bằng 360 độ.
Tứ giác có thể là lồi hoặc lõm. Nếu tất cả các góc trong đều nhỏ hơn 180 độ thì gọi là tứ giác lồi, còn nếu có một góc lớn hơn 180 độ thì gọi là tứ giác lõm.
Tứ giác có thể được phân loại thành nhiều dạng đặc biệt như: hình thang, hình bình hành, hình chữ nhật, hình vuông, hình thoi, hình thang cân… Mỗi loại đều có những tính chất riêng biệt.
Vai trò của tứ giác trong hình học
Tứ giác là nền tảng quan trọng trong chương trình toán học, đặc biệt ở bậc trung học cơ sở và trung học phổ thông. Việc học khái niệm và đặc điểm của tứ giác giúp học sinh phân biệt các loại tứ giác đặc biệt, nắm vững công thức tính diện tích, chu vi và áp dụng trong các bài toán chứng minh hình học.
Khái niệm về diện tích tứ giác
Tứ giác là hình phẳng được tạo thành bởi bốn cạnh nối liền bốn điểm phân biệt. Việc tính diện tích tổng quát phức tạp hơn so với tam giác, vì hình có thể không đều và không đối xứng. Để tính chính xác diện tích, cần dựa vào các công thức hình học phù hợp với dữ liệu đã cho.
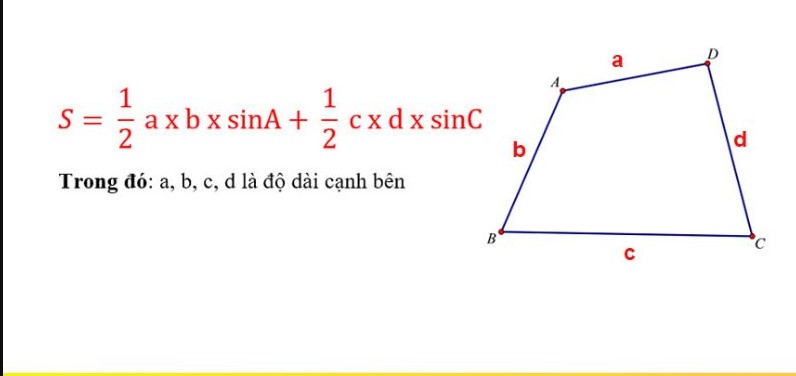
Công thức diện tích tứ giácTrong xây dựng và kiến trúc
Việc tính diện tích được áp dụng nhiều trong thiết kế công trình. Khi đo đạc mặt bằng hay phân chia đất đai, các khu đất thường có hình dáng không đều, đôi khi là tứ giác. Kỹ sư xây dựng và kiến trúc sư dựa vào công thức diện tích để tính toán diện tích chính xác, từ đó lên kế hoạch thi công, phân bổ vật liệu và xác định chi phí hợp lý.
Trong quy hoạch đất đai và bất động sản
Khi đo vẽ bản đồ địa chính, nhiều mảnh đất có hình dạng gần giống tứ giác. Việc tính toán diện tích giúp xác định rõ ràng ranh giới, hạn mức sử dụng và giá trị mua bán. Đây là ứng dụng quan trọng trong quản lý nhà đất, đảm bảo tính minh bạch và công bằng khi giao dịch bất động sản.
Trong học tập và nghiên cứu
Việc tìm diện tích giúp học sinh, sinh viên rèn luyện kỹ năng tư duy logic và vận dụng công thức hình học. Các dạng bài tập tính diện tích không chỉ củng cố kiến thức mà còn giúp người học hình dung rõ ứng dụng toán học trong thực tế. Đối với những ngành nghiên cứu như địa lý, quy hoạch đô thị hay kiến trúc cảnh quan, công thức tính diện tích là công cụ cần thiết.
Trong thiết kế nội thất và trang trí
Nhiều vật dụng hoặc khu vực trong nhà có thể được quy về hình tứ giác như mặt bàn, khung cửa, khu vực lát gạch. Việc tính diện tích chính xác giúp chọn số lượng vật liệu phù hợp, tránh lãng phí và đảm bảo tính thẩm mỹ trong trang trí.
Trong sản xuất và đời sống hàng ngày
Trong nông nghiệp, khi tính toán diện tích ruộng vườn, người nông dân thường gặp những mảnh đất có hình tứ giác. Nhờ biết cách tính diện tích, họ có thể xác định chính xác diện tích canh tác, từ đó dự đoán sản lượng và phân bổ giống, phân bón hiệu quả. Trong đời sống thường nhật, việc tính diện tích tứ giác cũng giúp chúng ta khi đo đạc, thiết kế, hay sửa chữa nhà cửa, sân vườn.
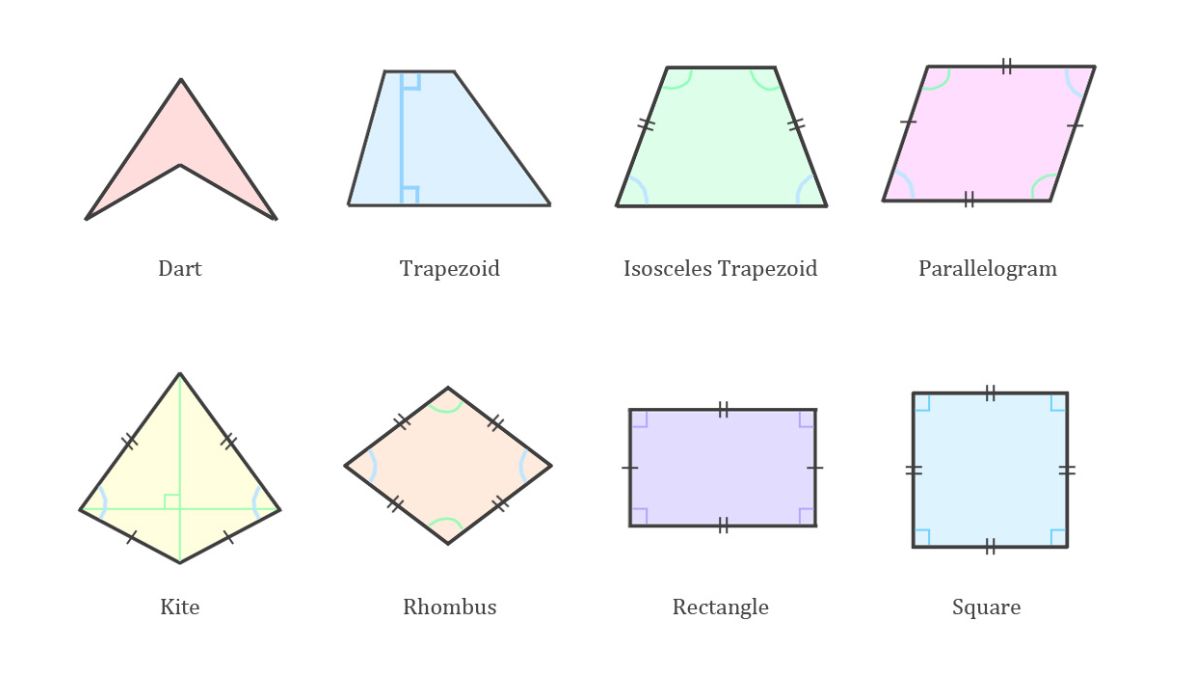
Các loại hình tứ giácHình vuông
Hình vuông là tứ giác có bốn cạnh bằng nhau và bốn góc vuông. Đây là dạng đặc biệt và đối xứng nhất trong các loại tứ giác. Trong đời sống, hình vuông xuất hiện ở viên gạch lát, tấm khăn giấy hay các khối lập phương trong hình khối ba chiều.
Hình chữ nhật
Hình chữ nhật có hai cạnh dài và hai cạnh ngắn song song bằng nhau, đồng thời có bốn góc vuông. Đây là dạng tứ giác dễ nhận biết và có nhiều ứng dụng, chẳng hạn như trong sách vở, bảng học, màn hình tivi hay điện thoại.
Hình thang
Hình thang là tứ giác có ít nhất một cặp cạnh đối song song. Hình thang cân là trường hợp hai cạnh bên bằng nhau, còn hình thang vuông có một cạnh bên vuông góc với cạnh đáy. Trong thực tế, hình thang thường thấy trong kiến trúc, thiết kế hoặc mặt cắt của nhiều công trình.
Hình bình hành
Hình bình hành có hai cặp cạnh đối song song và bằng nhau. Nếu hình bình hành có góc vuông, ta được hình chữ nhật; nếu có bốn cạnh bằng nhau, ta được hình thoi. Đặc điểm này giúp hình bình hành trở thành cơ sở để suy luận ra nhiều dạng tứ giác đặc biệt khác.
Hình thoi
Hình thoi có bốn cạnh bằng nhau, hai đường chéo vuông góc và cắt nhau tại trung điểm. Đây là dạng đặc biệt vừa mang tính chất của hình bình hành, vừa có nét tương đồng với hình vuông nhưng không bắt buộc có góc vuông.
Tứ giác bất kỳ
Tứ giác bất kỳ không tuân theo một quy tắc cố định nào về cạnh hoặc góc. Loại này thường được chia thành hai tam giác để dễ phân tích và tính toán. Trong tự nhiên và thiết kế sáng tạo, tứ giác bất kỳ xuất hiện rất nhiều.