Thể tích khối lập phương
Hình lập phương là khối hình học không gian đặc biệt có 6 mặt, 8 đỉnh, 12 cạnh, tất cả các mặt đều là hình vuông bằng nhau và các cạnh lập phương có độ dài bằng nhau.
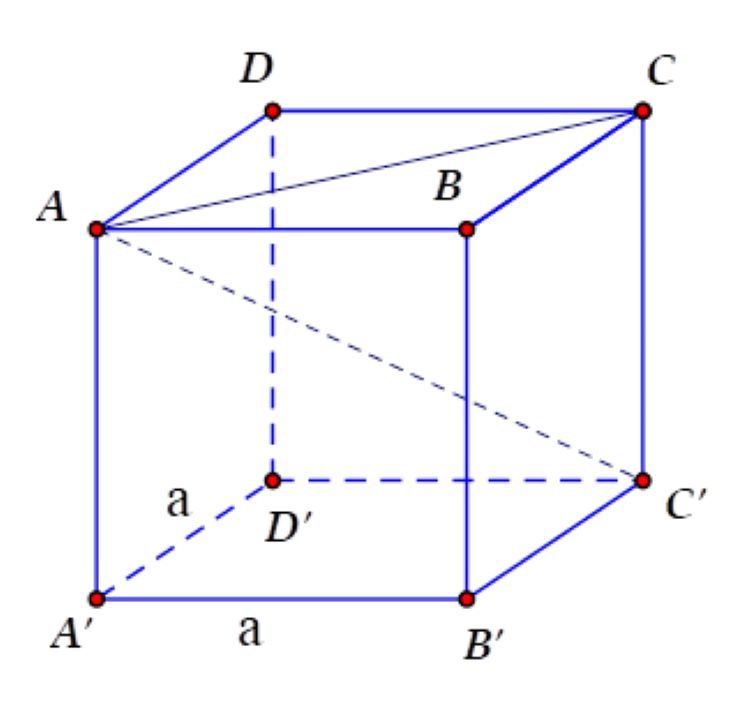
Tính chất của hình lập phương
Tính chất của một hình lập phương:
Có 6 mặt phẳng bằng nhau
Có 12 cạnh bằng nhau
Đường chéo của tất cả các mặt đều có độ dài bằng nhau
Công thức tính thể tích khối lập phương:
Để tính thể tích hình lập phương ta lấy độ dài ba cạnh nhân với nhau. Hay thể tích hình lập phương chính bằng lập phương của 1 cạnh.
Công thức được viết như sau: V = a^3= a x a x a
Trong đó:
V là thể tích hình lập phương (có đơn vị là cm³, m³,....)
a là độ dài các cạnh của hình lập phương
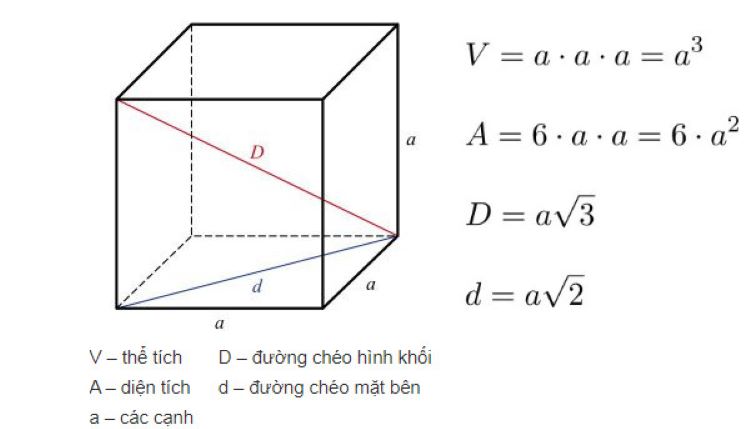
Công thức tính thể tích khối lập phương
Ví dụ minh họa:
Ví dụ 1: Cho hình lập phương ABCDA’B’C’D’ có cạnh a = 4cm. Tính thể tích của hình lập phương?
Ta có V = 4 x 4 x 4 = 64 cm³
Ví dụ 2: Cho một hình lập phương V1 có các cạnh độ dài bằng nhau và bằng 7 cm. Hỏi thể tích của hình lập phương V1 này bao nhiêu?
Giải
Ta có các cạnh của hình lập phương bằng nhau và bằng một giá trị a = 7 cm.
Áp dụng công thức tính thể tích khối lập phương ta có:
V1 = a^3 = 7 ^3 = 343 cm3
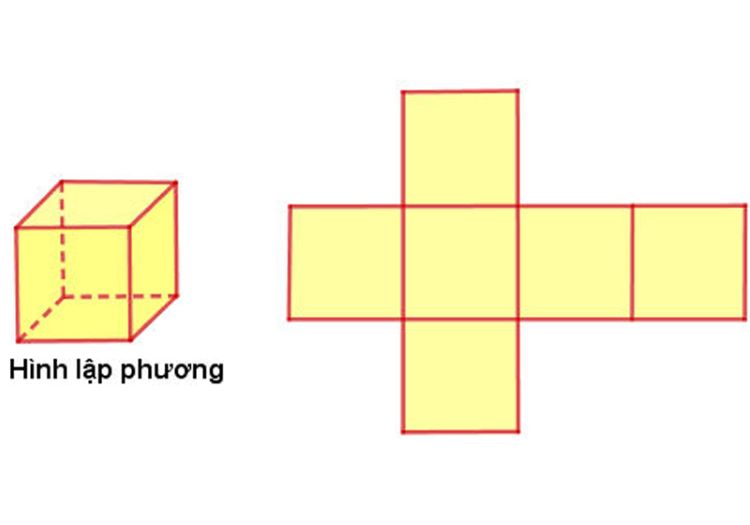
Một số dạng bài áp dụng thể tích hình lập phương
>> Xem thêm: Diện tích tam giác vuông cân
Dạng 1: Tính thể tích của hình lập phương khi đã biết độ dài
Cách giải: Với dạng bài này, ta chỉ cần áp dụng công thức tính: V = a x a x a để tính thể tích hình lập phương
Ví dụ: Cho hình lập phương có chiều dài các cạnh là 6 cm. Tính thể tích của hình lập phương đã cho.
Giải: Áp dụng công thức thể tích: V = a x a x a = 6 x 6 x 6 = 216 cm³
Vậy thể tích của hình lập phương là 216 cm³
Dạng 2: Tính thể tích hình ập phương khi đã biết diện tích xung quanh hoặc diện tích toàn phần.
Cách giải:
Nếu đề bài cho biết diện tích xung quanh, bạn áp dụng công thức để tính độ dài một cạnh: Sxq = 4 x a x a=> a^2 = Sxq/4
Nếu đề bài cho biết diện tích toàn phần,bạn áp dụng công thức để tính độ dài 1 cạnh: Stq = 6 x a x a => a^2 = Stp / 6
Sau khi tính độ được độ dài canh, bạn áp dụng công thức tính thể tích là xong.
Ví dụ: Cho hình lập phương biết diện tích xung quanh là 25 cm2. Tính thể tích của hình lập phương đã cho.
Giải: Diện tích xung quanh là 100 cm2 => Sxq = 100 = 4 x a x a => 25 = a x a => a = 5 cm. Độ dài các cạnh của hình lập phương đã cho là 5 cm.
Vậy thể tích của hình lập phương trên là: V = a x a x a = 5 x 5 x 5 = 125 cm³
Dạng 3: Tính độ dài của cạnh khi biết thể tích
Cách giải: Nếu đi tìm một cạnh a mà đã biết a x a x a = V thì độ dài cạnh hình lập phương chính là a. Hay chính là căn bậc 3 của V.
Ví dụ: Cho hình lập phương với thể tích V là 64 cm³. Tính độ dài cạnh của hình lập phương trên.
Giải: Độ dài một cạnh của hình lập phương là V = a x a x a = 64 => a = 4 cm
Dạng 4: So sánh thể tích của một hình lập phương này với thể tích của một hình lập phương khác
Cách giải: Áp dụng công thức tổng quát để tính thể tích từng hình rồi đem ra so sánh.
Lưu ý: Cần đảm bảo hai hình lập phương có cùng chung đơn vị đo độ dài. Sau đó mới tiến hành so sánh.
Bài 1: Tính thể tích hình lập phương với cạnh bằng 3 dm
Giải
Thể tích của hình lập phương đó là:
3 x 3 x 3 = 27 cm³
Đáp số: 27 cm³
Bài 2: Một khối kim loại hình lập phương có độ dài cạnh là 0,4m, mỗi dm³ kim loại đó có cân nặng 15 kg. Hỏi khối kim loại này có cân nặng bao nhiêu kg?
Phương pháp giải:
Trước hết: Tính thể tích khối kim loại, áp dụng công thức.
Đổi thể tích vừa tìm được sang đơn vị là dm³
Tính cân nặng của một khối kim loại này bằng cách ta lấy cân nặng của mỗi Đề-xi-mét khối nhân với thể tích của khối kim loại trên..
Lời giải:
Thể tích của khối kim loại hình lập phương là:
V= 0,4 x 0,4 x 0,4 = 0,064 m3
Đổi 0,064 m³ = 6,4 dm³
Khối kim loại đó có cân nặng số kg là:
15 x 6,4= 96 kg
Đáp số: 96 kg
Bài 3: Phải xếp bao nhiêu hình lập phương nhỏ với cạnh 1cm để được một hình lập phương lớn với diện tích toàn phần là 294dm²
Giải:
Diện tích một mặt của hình lập phương lớn là: a^2= Stp/6 = 294 : 6 = 49 dm
Có 49 = 7 x 7 nên độ dài cạnh hình vuông lớn là 7dm = 70cm
Thể tích của hình lập phương lớn là V1= 70 x 70 x 70 = 343000 cm³
Thể tích của hình lập phương nhỏ là 1 x 1 x 1 = 1cm³
Vậy sẽ cần tổng là 343000 hình lập phương nhỏ.
Trên đây là những thông tin chi tiết về công thức tính thể tích hình lập phương và bài tập áp dụng. Hy vọng bài viết đã cung cấp những thông tin hữu ích cho bạn đọc, chúc bạn áp dụng thành công.