Diện tích tứ giác
Tứ giác là gì trong hình học
Trong hình học phẳng, tứ giác là hình có bốn cạnh và bốn đỉnh. Đây là một trong những dạng hình học phổ biến nhất, bao gồm nhiều loại quen thuộc như hình vuông, hình chữ nhật, hình thang, hình thoi hay hình bình hành. Mỗi loại tứ giác lại có những công thức tính diện tích riêng, dựa trên đặc điểm về cạnh, góc và đường chéo.
Ý nghĩa của việc tính diện tích hình tứ giác
Diện tích tứ giác là phần mặt phẳng được bao bọc bởi bốn cạnh của hình. Việc tính diện tích có vai trò quan trọng không chỉ trong việc học tập mà còn trong ứng dụng đời sống. Khi cần đo đạc đất đai, thiết kế kiến trúc hay làm bài toán kỹ thuật, bạn sẽ thường xuyên gặp những hình có dạng tứ giác. Hiểu cách tính diện tích hình tứ giác sẽ giúp tiết kiệm thời gian, tính toán chính xác và áp dụng linh hoạt trong nhiều tình huống.
Hình tứ giácCông thức áp dụng cho tứ giác đặc biệt
Một số tứ giác đặc biệt có công thức diện tích đơn giản. Với hình vuông, diện tích được tính bằng cạnh nhân cạnh. Với hình chữ nhật, diện tích bằng chiều dài nhân chiều rộng. Với hình thoi, diện tích được tính bằng tích hai đường chéo chia đôi. Với hình bình hành, diện tích bằng cạnh đáy nhân chiều cao. Những công thức này dễ nhớ, dễ áp dụng và thường xuyên được sử dụng trong chương trình toán tiểu học và trung học.
Công thức tính diện tích hình tứ giác bất kỳ
Trong trường hợp tứ giác không thuộc các loại đặc biệt, ta có thể áp dụng công thức Bretschneider. Công thức này viết như sau: S=√ ((p - a)(p - b)(p - c)(p - d) - abcd × cos² ((A + C)/2)) Trong đó, a, b, c, d là bốn cạnh của tứ giác, A và C là hai góc đối diện, p là nửa chu vi bằng (a + b + c + d)/2. Công thức này tuy phức tạp hơn nhưng cho phép tính diện tích mọi tứ giác bất kỳ khi biết bốn cạnh và một cặp góc đối diện.
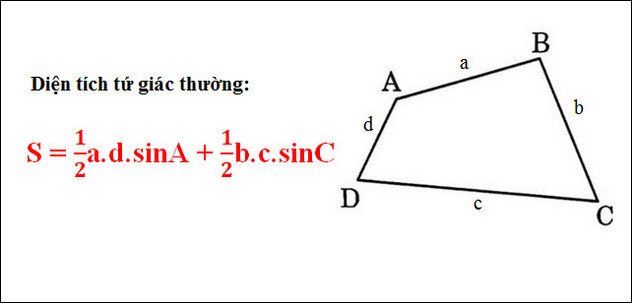
Diện tích hình tứ giácVí dụ với tứ giác đặc biệt
Giả sử bạn có một hình chữ nhật với chiều dài bằng mười mét và chiều rộng bằng sáu mét. Diện tích của hình chữ nhật này sẽ là mười nhân sáu bằng sáu mươi mét vuông. Nếu hình thoi có đường chéo dài tám mét và đường chéo còn lại sáu mét, diện tích sẽ bằng tích của hai đường chéo chia hai, tức là hai mươi bốn mét vuông. Những ví dụ này cho thấy việc tính diện tích hình tứ giác đặc biệt khá dễ dàng.
Ví dụ với tứ giác bất kỳ
Giả sử có một tứ giác với bốn cạnh lần lượt là năm, sáu, bảy và tám đơn vị, cùng với hai góc đối diện A và C có tổng bằng một trăm tám mươi độ. Khi đó, công thức Bretschneider sẽ rút gọn thành công thức Brahmagupta dành cho tứ giác nội tiếp. Nửa chu vi p bằng (5 + 6 + 7 + 8)/2=13. Khi áp dụng công thức, diện tích S=√ ((13 - 5)(13 - 6)(13 - 7)(13 - 8)). Kết quả là √ (8 × 7 × 6 × 5)=√ 1680 ≈ 40, 99 đơn vị vuông. Qua ví dụ này, bạn có thể thấy công thức diện tích hình tứ giác có thể giải quyết cả những trường hợp phức tạp.
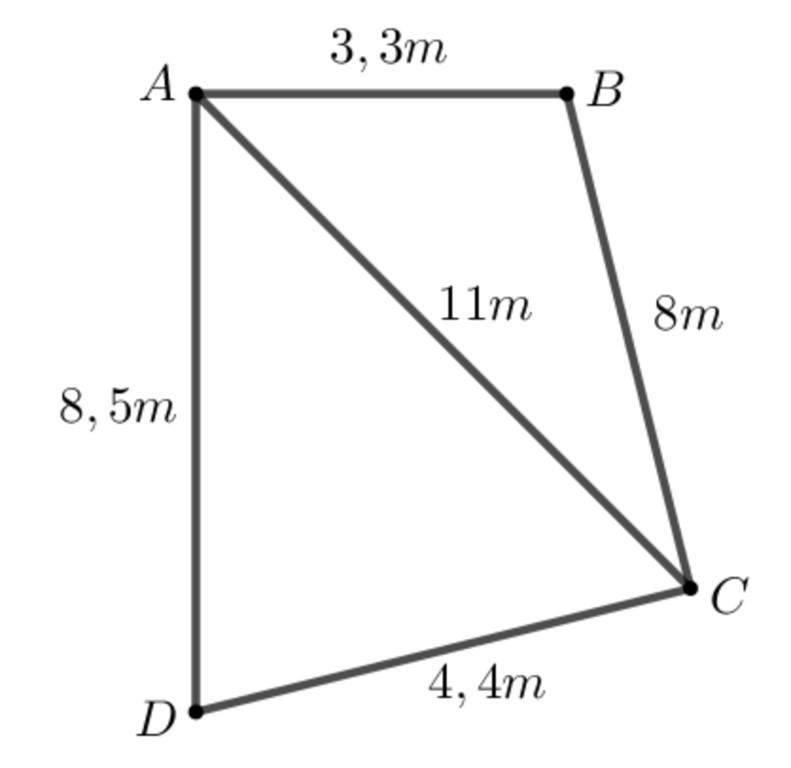
Tứ giácỨng dụng trong giáo dục và thi cử
Trong chương trình toán học, các bài toán liên quan đến diện tích hình tứ giác xuất hiện thường xuyên. Học sinh không chỉ áp dụng công thức cơ bản mà còn phải linh hoạt sử dụng nhiều phương pháp khác nhau như chia tứ giác thành hai tam giác rồi tính diện tích từng phần. Việc luyện tập thường xuyên sẽ giúp nắm chắc công thức, tăng khả năng tư duy logic và giải quyết bài toán hiệu quả.
Ứng dụng trong xây dựng và đời sống
Trong đời sống thực tế, nhiều bề mặt hoặc mảnh đất có hình dạng gần giống tứ giác. Một căn phòng, một mảnh đất vườn hoặc một tấm kính cửa sổ đều có thể là tứ giác. Khi muốn lát gạch, trải thảm hoặc đo diện tích để xây dựng, việc tính diện tích hình tứ giác trở nên vô cùng hữu ích. Nhờ áp dụng công thức, người thiết kế có thể tính toán lượng vật liệu cần thiết, tiết kiệm chi phí và tránh lãng phí.>> Tham khảo: bạt chống cháy khi hàn Tránh sai sót khi tính toán
Sai lầm thường gặp là nhầm lẫn đơn vị đo hoặc quên quy đổi về cùng một hệ. Nếu chiều dài đo bằng mét còn chiều rộng tính bằng xăng ti mét mà không quy đổi, kết quả sẽ sai lệch. Một lỗi khác là nhầm giữa đường chéo và cạnh khi áp dụng công thức hình thoi hoặc công thức tổng quát. Vì vậy, trước khi tính toán, bạn cần xác định rõ yếu tố cần thiết và đặt về cùng một đơn vị đo.
Mẹo học nhanh công thức
Một cách dễ nhớ là liên hệ diện tích hình tứ giác với diện tích tam giác. Khi chia tứ giác thành hai tam giác qua đường chéo, bạn có thể tính diện tích từng tam giác rồi cộng lại. Với cách này, nếu nhớ được công thức diện tích tam giác theo Heron, bạn sẽ dễ dàng mở rộng sang công thức diện tích hình tứ giác. Cách liên hệ logic này giúp ghi nhớ lâu hơn và áp dụng linh hoạt trong nhiều tình huống khác nhau.
Diện tích tứ giác là một trong những kiến thức quan trọng của hình học phẳng. Dù là tứ giác đặc biệt như hình vuông, chữ nhật hay tứ giác bất kỳ, chúng ta đều có những công thức phù hợp để tính toán. Khi nắm vững công thức và luyện tập thường xuyên, bạn không chỉ học tốt môn toán mà còn áp dụng vào nhiều lĩnh vực thực tế như đo đạc, xây dựng và thiết kế. Hãy bắt đầu từ các ví dụ đơn giản rồi dần dần luyện tập với những trường hợp phức tạp để thành thạo cách tính diện tích hình tứ giác.